Random Thoughts – Randocity!

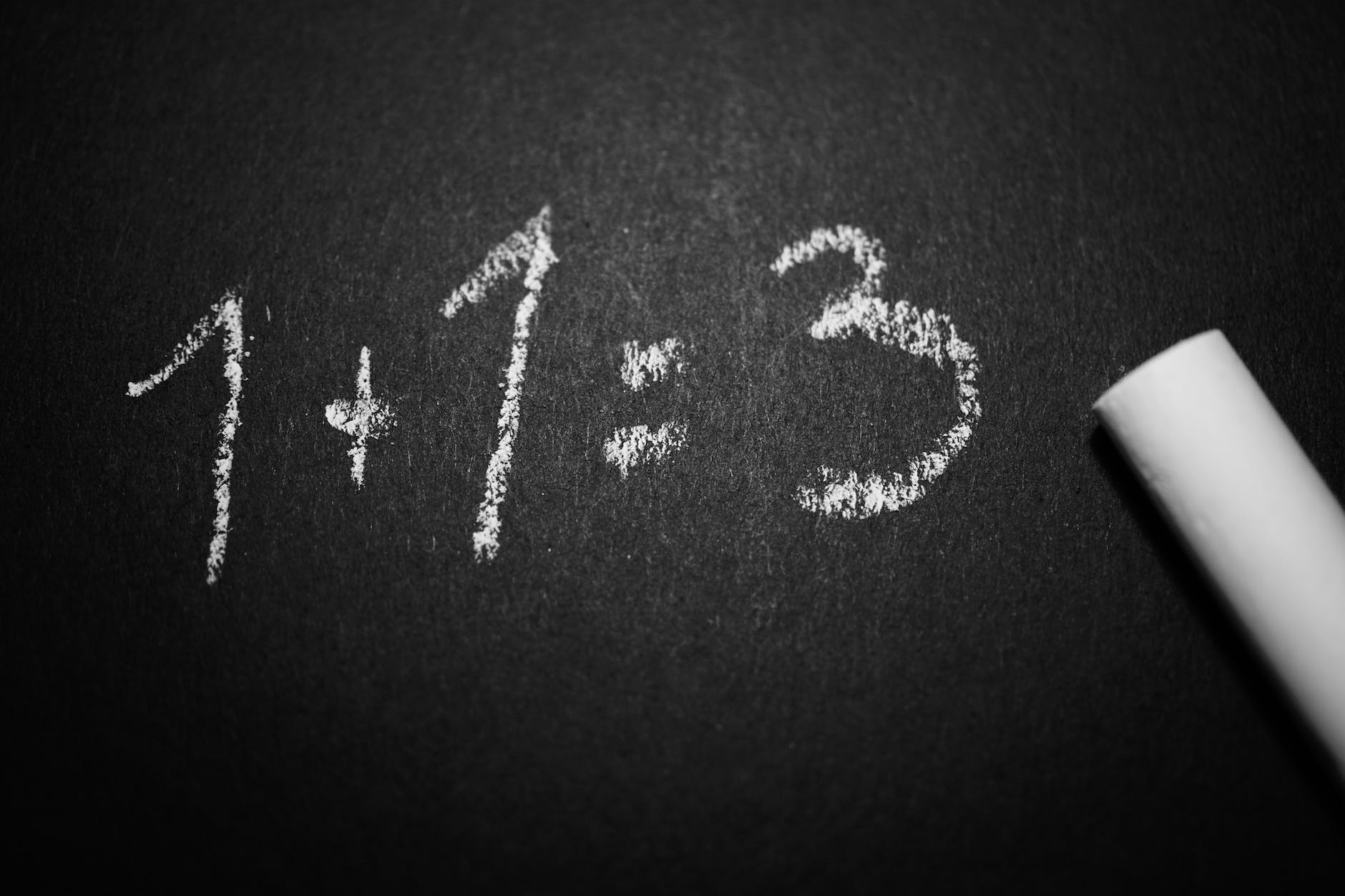
Many puzzles that pop up on many social media networks are math problems. One of these older math “problems” is 6 ÷ 2(1 + 2). Let’s explore the difficulties and controversies surrounding this math problem.

PEMDAS, BODMAS, BIDMAS & BEDMAS

These are all acronyms for more or less the same ideology. This ideology is intended to help students solve math problems logically. Unfortunately, PEMDAS and its similar ilk all have problems when it comes to certain advanced mathematical constructs… constructs that are, in fact, intentionally ignored in PEMDAS for the sake of simplicity.

PEMDAS stands for Parenthesis, Exponents, Multiplication and Division, Addition and Subtraction. BODMAS, BIDMAS and BEDMAS all utilize this same ideology, using alternative words to describe these approaches to logical math problem solving. Interestingly enough, BODMAS, BIDMAS and BEDMAS all seem to place division before multiplication, unlike PEMDAS. However, multiplication and division, at least according these problem solving helpers are supposed to be equal and performed strictly in order from left to right. In effect, the ‘DM’ order in BODMAS (and similar) or ‘MD’ order in PEMDAS make no real difference because the math problem itself dictates the order in which to solve the problem, left to right. In other words, the order takes precedence, so the ‘DM’ or ‘MD’ order listed in these helpers don’t matter.

Why PEMDAS or similar?

The PEMDAS and similar helpers were created to help grade school students solve basic math problems. This would include simple math problems like 10 ÷ (5 – 3)  or (5 + 2 – 1) x 2. For those unfamiliar, the ⇝ symbol should be read as “which leads to.”

For the first problem 10 ÷ (5 – 3) that would be solved by the helpers with the following:

Parentheses first: (5 – 3) = 2 ⇝ 10 ÷ (2)
Next drop the parentheses, then solve for MD/DM: 10 ÷ 2 = 5
Answer: 5

For the second problem (5 + 2 – 1) x 2

Parentheses solved first with + and – solved inside parens l-to-r: (5 + 2 – 1) = (6)
Drop parens, multiply  6 x 2 = 12
Answer: 12

These above are simple math problems that don’t involve one key concept included in the somewhat more advanced math problem 6 ÷ 2(1 + 2). The key math concept included is …

Multiplication by Juxtaposition (aka Implied Multiplication)

Multiplication by Juxtaposition adds a level of complexity that PEMDAS and BODMAS can’t always resolve. Let’s understand why.

Multiplication by juxtaposition is a concept that gets introduced during a student’s first Algebra class. Prior to taking algebra, the concept of implied multiplication isn’t involved. PEMDAS wasn’t designed to adequately support this advanced math concept. PEMDAS, thusly, isn’t the whole truth. PEMDAS is a ruleset that works for many math problems, but not for ALL math problems. This is why PEMDAS trips up many people when attempting to use it on problems like 6 ÷ 2(1 + 2).

Before getting into this specific math problem, let’s understand a few more implied multiplication examples. An implied multiplication example is , which means 2 times a times b or . If a = 5 and b = 2, the problem and answer would look like . Note that * = x = times. A somewhat complex algebraic equation might be . Solving this problem would be relatively easy as long as we know what x, y, a and b are.

The point here is not to get deep in the weeds of algebra, but instead to understand the intricacies of multiplication by juxtaposition when used in combination with PEMDAS. Juxtaposition is illustrated in problem like . Because ‘a’ and ‘b’ sit directly next to one another with nothing in between, this juxtaposition implies multiplication between these two variables. The point is, juxtaposition written in this way always implies multiplication.

Juxtaposition is a method of writing equations without the need to include the * or x symbols which explicitly state multiplication. When choosing to use juxtaposition instead of explicit symbols, this is what is called using a “style guide” for mathematical equations.

Like map legends are used to describe such information as color coding and distances on maps, style guides in mathematics describe the proper order that an equation needs to solved. Why is a style guide important? Because of the ambiguities and disparities between PEMDAS and writing equations using these shorthand methods, such as juxtaposition.

Juxtaposition is intended to help simplify the printing of equations in printed texts as well as reduce the clutter when building such complex equations. When complex equations are written, then, a style guide reference discussing precedence, levels and order of operation is imperative. Without this information printed alongside a text book, this would leave the reader in the dark, forcing the reader to utilize their own knowledge to attempt to solve the written problem.

This is exactly the problem with the Facebook problem in 6 ÷ 2(1 + 2). Because no style guide is offered, this math problem has two valid solutions; solutions that depend on which style guide you are familiar. If you subscribe to only the PEMDAS helper style guide, the answer is 9. If you subscribe to the vast majority of scientific and technical literature style guides used by STEM professionals, the answer is 1.

Let’s understand why

6 ÷ 2(1 + 2) can be written in effectively two different ways depending on which style guide you choose. The PEMDAS style guide implies the following style should be applied:

6 ÷ 2 * (1 + 2), alternatively written as .

Mathematical professional style guides would apply the following:

6 / (2 * (1 + 2)) (adding another set of parentheses for clarification)

Let’s understand these styling differences.

Under PEMDAS styling, the equation is understood as:

or more specifically,

Using scientific and engineering style guide rules, the equation is understood as:

These two equations are markedly different both in their appearance, but also in how they are solved. Under PEMDAS styling, the answer is clearly 9. Under scientific styling the answer is obviously 1.

The question is, why are there two different style guides here?

Two Style Guides?

PEMDAS (et al) is a rudimentary style guide intended to teach grade school children mathematic basics. PEMDAS is not intended to carry the child’s mathematical knowledge all the way through their life. Think of PEMDAS like a set of training wheels on your bike. The training wheels keep you upright to get the hang of balancing on your bike. Once you’ve mastered the art of balancing, the training wheels are removed.

PEMDAS is simply a set of training wheels that eventually need to be removed.

To be perfectly fair, PEMDAS should really be written as . The PEMDAS style guide is effectively 4 components, not 6.

This updated 4 component notation means MD are at the same level and equal priority, but evaluated in order left to right. AS follows the same logic as MD, but only after MD have been resolved.

The difficulty with PEMDAS is that it was designed to be used by students NOT working with either multiplication by juxtaposition (implied multiplication — an algebra concept) or by using a slash (/) in place of the division (÷) symbol (also an algebra concept). PEMDAS expects the primary four simple operators to be explicitly used: + – ÷ x. PEMDAS breaks down when advanced operators are used because PEMDAS has no proper solution when these advanced mathematical concepts are included.

The reason for these existence of these two style guides goes back to the history of order of operations, long before even PEMDAS was coined. Most engineering and mathematics texts define that multiplication by juxtaposition is to be handled BEFORE division. In PEMDAS terms, that means the acronym becomes where J stands for implicit multiplication by juxtaposition. When the J enters the PEJMDAS ideology, this Facebook equation is understood as:

instead of the PEMDAS understanding as

What does the division symbol ÷ mean exactly?

If you look at the ÷ symbol, it has a dot on the top and a dot on the bottom. As an abstract visual, it means “divide by”. As a literal symbol, it means move the left argument to the numerator and the right argument to the denominator. This turns 6 ÷ 2 into . Thus, the entire ÷ symbol itself is representative of defining a fraction. For ease of teaching fractions more simply, the ÷ symbol was devised to aid learners in conceptually grasping division better without involving something that visually looks like this: in every single math problem involving division. 10 ÷ 2 is way more palatable both visually and conceptually than . Thus, the reason the division symbol ÷ was born.

The ÷ symbol also has a sibling, the forward slash (/). This slash symbol can be used as a drop-in replacement for the ÷ symbol. When a slash is used, this then represents the two numbers as a sort of sideways or horizontal fraction, like 6/2. In STEM professional circles, both the ÷ and the x symbols are exchanged for alternatives when writing equations. Think of these changes as mature upgrades to mathematics. As we grow and learn, we adopt shortcuts which make life easier. In mathematics, juxtaposition and slash are two mature “shortcuts” in the way that equations get written. Instead of writing an equation as 6 ÷ 2(1+2), it would be written as 6/2(1+2) or if using TeX, it would appear more formally as .

Why are there TWO answers?

Good question. One that needs all of the above understanding to address. Style guides vary. The PEMDAS style guide given to early grade school students is intended to be used as a loose style guide only. Meaning, given our rudimentary understanding of mathematics at the time, PEMDAS is a helper tool that “guides” us in the right direction. PEMDAS isn’t an end-all be-all idea. It is simply a helper tool. If mathematical equations ended at the type given to us in grade school, PEMDAS is all that we would ever need.

However, moving into Algebra and higher mathematics like Trigonometry and Calculus, mathematical nomenclature must become more refined and mature… and so it does. In that goal, what PEMDAS taught us was basics. What we learn in advanced mathematics classes overrides what we learned with the basic PEMDAS logic.

Because math style guides acknowledge that there are more priority levels than the simple PEMDAS understands, our knowledge of PEMDAS must expand into that bigger understanding of more priority levels. We must take off the PEMDAS training wheels and let go of the past. We must acknowledge that there is more to mathematics than PEMDAS.

PEJMDAS is a good first step, but it doesn’t explain everything. For example, why does PEMDAS view the equation 6 ÷ 2(1+2) as instead of ?

The answer to this is really pretty simple. PEMDAS places ALL multiplication at the same level and priority as under the M. Because PEMDAS isn’t really aware of juxtaposition rules, it mistakenly moves even juxtaposed multiplication under M. PEMDAS then mistakenly turns the equation into .

The problem is that PEMDAS is taught at a time in school when juxtaposed multiplication isn’t even a concept in mathematics. As a result of juxtapositioning not being understood at that moment in a student’s mathematical learning, the student would then assume, based on PEMDAS, that ALL multiplication must roll up under that M… that’s assuming the student even understands or had been previously explained about implied multiplication. Most students learning early mathematics would likely have to ask what 6 ÷ 2(1 + 2) means. More specifically, why is a 2 sitting directly next to the (1 + 2) parentheses without an operator symbol and also what it means in this equation? This is where juxtaposition multiplication would have to be explained to the student.

In reality, in many advanced academic mathematical style guides, something that a grade school student would not be aware of, these documents state that multiplication by juxtaposition must be calculated BEFORE division. With this academic rule in place, that changes 6 ÷ 2(1 + 2) into the more widely understood and accepted .

Why is there even a question here?

Many insist that 9 is the correct answer. Yet, just as many insist that 1 is the correct answer. The disparity between these two camps comes because of one simple disagreement in math priority; a math priority that is defined by many academic and professional texts. Even many calculators have adopted this math priority rule as genuine and valid. The disparity whether multiplication by juxtaposition happens BEFORE division or whether it happens only when all general multiplication occurs in an equation is what gives rise to this equation’s dilemma.

When equations are not written in a left to right format, such as in , left to right cannot be utilized except where specifically applicable. Left to right can only be utilized IF the math problem is written using a fully left-to-right format like 6 ÷ 2(1+2).  Even then, because the ÷ can be interchanged with /, a person who changes ÷ to / could then adopt the idea that 6 / 2(1 + 2) is the same as .

Why? Because many academic style guides adopt the rule that when using a slash (/) to describe division in an equation, equations like 6 / 2(1 + 2) become the same as , thus making this equation not the same as . In these style guides, it seems that implied parentheses are removed. For example, 6 / (2(1 + 2)) explicitly defines . However, many mathematical style guides eliminate spurious parentheses for clarity and brevity, but they are still effectively there. In the case of this equation, adding that extra set of parentheses is actually more or less pointless because these academic style guides generally agree that EVERYTHING on the left side of the slash goes into the numerator and EVERYTHING on the right side of the slash also goes into the denominator unless there is an explicit * multiplication (or other operator) symbol present.

For example, 6 / 2 * (1 + 2) translates into , but only because the explicit * symbol is present, which prevents everything after the * from going into the denominator. When juxtaposition is in play, the previous paragraph’s rule applies.

Standards in Mathematics

What this article all boils down to is a failure to create a common ruleset of standards that everyone across all mathematical areas agree to. Thankfully, all areas of STEM professions agree by including style guide information when applicable. These style guide rules prevents confusion and misinterpretation on how to read and solve equations in a professional setting, such as in engineering, architecture and other critical areas.

What 6 ÷ 2(1+2) uncovers is the lack of generally agreed upon standards outside of professional environments. Grade school teachers and students believe that 9 is the correct answer because they’ve never been taught and have never used the style guides used by STEM professionals. On the flip side, STEM professionals don’t use PEMDAS as their leading style guide ever in their professional careers. Instead, because academia has defined specific priorities and rules regarding multiplication by juxtaposition, rules which many calculator manufacturers have adopted, this Facebook math problem only serves to uncover who was taught what.

Someone probably realized the disparity between the guide a STEM professional uses and the PEMDAS (et al) style guide(s) grade school teachers use. Then, this person decided to exploit this situation by creating this equation dilemma as a joke.

In reality, this equation only serves to show us all that consistent standards don’t exist even in mathematical circles. More than this, it shows that grade school math alone isn’t enough understand that there are two answers to this equation, with both answers being completely correct. In other words, this equation intentionally serves to disclose who follows PEMDAS and who follows more advanced mathematical style guides.

Calculator Dilemma

Some calculator manufacturers support PEMDAS, but many more support PEJMDAS as described above. As a result, unless you explicitly read the calculator user manual before you buy it, you may not understand why your calculator seems to be giving you the wrong results. In reality, it’s not giving you the wrong results. It’s giving you those results because of the disparity between the two differing style guides in use within different mathematical circles.

What does this all mean?

It means that there is no consistent teaching of the order of operations rules across all math classes across the globe. Because there are effectively two camps of people who were taught different orders of operation at differing priorities, your best bet is to write unambiguous math problems; problems that can’t have two potential answers. To do this, you’ll need to be aware of the above disparity in how order of operation is taught in mathematics in differing locations and under various instructors. Until you acknowledge that there is inconsistency in this area of mathematics, you can’t work around this problem.

The way to avoid such ambiguous problems as 6 ÷ 2(1 + 2), you can either write the problem more specifically like or you can put more parentheses into the left-to-right version of the equation so there is no difficulty for students who might have been taught a different approach. If you’re an “answer is 1” person, then write it as 6 ÷ (2 (1 + 2)). If you’re an “answer is 9” person, write it as (6 ÷ 2) * (1 + 2). Leave no question about which style to use to solve the equation.

If you are one of those stubborn folks who believes that there is and can only ever be once correct answer. Sorry to pop your bubble, but in this reality, there are technically two answers based entirely upon which style guide you adopt and/or which teacher taught you mathematics.

Are you a student?

A small disclaimer here for students. If you’re a student still in school reading this, know that there are two answers…. but also know that you need to follow your teacher’s lead. If your teacher is teaching you the “answer is 9” approach, always follow your teacher’s lead. The same goes for teachers who adopt “the answer is 1”. You want to get the best marks and that means catering to your math teacher’s approach. Know that there are two approaches that can work here, but don’t use the counter approach with your teacher unless you enjoy fighting with your teacher over your marks. As a general rule of thumb AND to make your school life a whole lot easier, always cater to your teacher’s wants, requests and whims to get the best marks and make them happy… even if you recognize those whims to be stupid.

As a student, be comfortable in your knowledge that you have recognized there are sometimes multiple ways of doing things. Know that there is absolutely nothing wrong in recognizing and booking this alternative knowledge. However, there is also no reason to fight with your instructors over knowing this information when it’s absolutely not necessary to get good marks in your class. Yes, you can be smart and know something your teacher may not. It’s also not necessary to pick a fight with your teacher over that knowledge. You never know how a teacher may respond when presented with information that’s contrary their lesson plans. You may find that many respond adversarially. It’s simpler to avoid this adversarial problem and go along with the lessons as written.

This is the trick to getting through school unscathed while also acknowledging the downsides and limitations of school curriculum. If you’re really interested in the above topic, wait until you’re in college to write and publish a paper on this very topic. Doing it this way, you can get college credit for disclosing such problems in your paper, but you can also get good grades from your teachers at the same time without being adversarial involving their teachings. Just make sure to write it for your English writing class and not as a paper for your math instructor, who might end up taking the paper far too personally or as an insult. It’s never a good idea to insult instructors, even if it’s through a well written, well researched paper.

Recap

To recap this article, the two answers for 6 ÷ 2(1 + 2) are 1 AND 9 respectively depending on which style guide you choose to adopt. Both style guides are entirely valid. Like map legends define what a map is telling you, a math style guide tells you how to solve any specific math problem.

If you are a student taking a mathematics class, only use the style guide your teacher permits. If you follow their style guide, you will always solve problems they give you with the correct answer. As for calculators, make sure the calculator you choose to buy also follows your instructor’s style guide. That means reading the calculator manual and, if possible testing the calculator. If the calculator doesn’t work as expected, return it for one that follows your teacher’s style guide.

↩︎